Piet Hein and the superellipse
An inspiration
A child of the sixties, I first encountered the superellipse in, I think, Scientific American. The curve was designer Piet Hein's compromise shape for a traffic roundabout in Stokholm.
What most intruigued me was that he had taken the familiar equation for a circle:
x^2 + y^2 = r^2
and looked at the family of curves which arise when the 2 was replaced by a variable, say p. That "2" had looked so solid and fixed. It turns out that the curve where p=2.5 elongated so that the ratio of the two axes was 3/4 was a compomise between a square and a circle which neatly fitted the space in Stockholm.
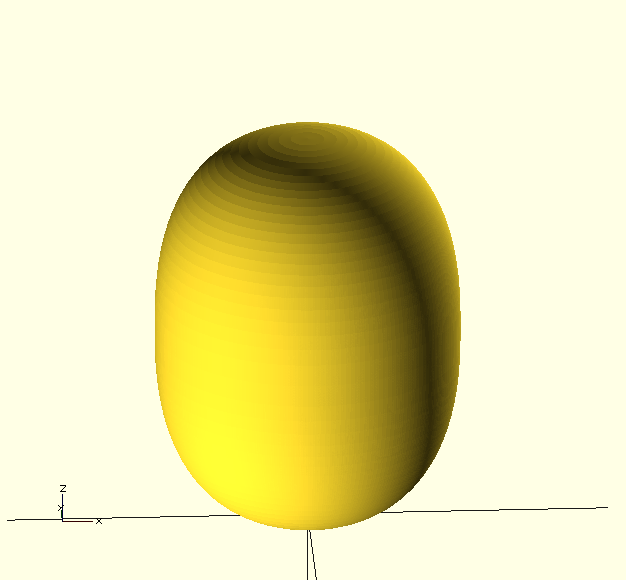
Moreover, when a solid is formed by revolving the shape, the resultant 'superegg' will, somewhat surprisingly, balance on its end. In fact I turned my own superegg from peach wood on my father's lathe which I still have.
Piet Hein became something of a hero for me. He was not only a mathematican and designer, he was a poet who had written numerous pithy 'Grook's whilst in the resistance in the second world war, was educated as a physicist. and was a friend of both Niels Bohr and Charlie Chaplin. He also invented numerous games and puzzles, including the Soma Cube.
The Road to Wisdom
The road to wisdom? .. Well, it's plain and simple to express.
Err
and err
and err again
but less
and less
and less.
Making a superegg
My attempts to create a superegg using OpenSCAD has been something of a journey. I first tried to generate the curve as a polygon. The main dificult is that vectors cannot be constructed dynamically so initally I used Python to calculate points on the curve at intervals, just as Piet Hein had done much more labouriously in 1959. The parametric equations come from Wikipedia. These were output in OpenSCD format.
from math import *;
import sys;
"""
eg. for Piet Hein's superegg
python superegg.py 20 2.5 0.75 > egg.scad
"""
def sign(x) :
return +1 if x >0 else -1
def shape(radius,p,roverh,max):
points = []
for i in range(0,max+1) :
theta = radians(360.0 * i/max)
y = radius * cos(theta)
x = roverh * radius * pow(abs(cos(theta)),2.0 /p) * sign(cos(theta))
y = radius * pow(abs(sin(theta)),2.0 /p) * sign(sin(theta))
points.append([x,y])
return points
def shape_openscad(radius,p,roverh,max) :
print "module shape() { translate([0,",str(radius),",0]) polygon("
print shape(radius,p,roverh,max)
print ");}"
radius = float(sys.argv[1])
p = float(sys.argv[2])
roverh = float(sys.argv[3])
shape_openscad(radius,p,roverh,100)
and a bit of OpenSCAD:
use <egg.scad>; $fa=0.01;$fs=0.5; shape();
and if we transform with rotate_extrude(), we get a superegg:
OpenSCAD curves
The Python/OpenSCAD approach works well and is fast to execute, but it would be better to use OpenSCAD alone so that we can vary p within a script to explore the superellipse family.
Looking around for scripts I found this thing which generated some roulette curves based on one circle rolling inside or outside another called trochoids. The OpenSCAD script seemed a bit daunting so I refactored one of the 2D shapes until I realised that the key parts were :
- functions to compute x and y values from a changing angle, theta
- approximating the area inside the curve by a number of adjacent segments
Each segment is a triangle [ [0,0], [xn, yn], [xn+1, yn+1] ]. OpenSCAD will assume the polygon is closed back to the first point and that the order of points on the curve is the same as the points in the list of points. To generate N segments, the N points on the curve have to be calculated twice because OpenSCAD does not allow variables to be updated, but such calculations are fast compared to the CSG computations.
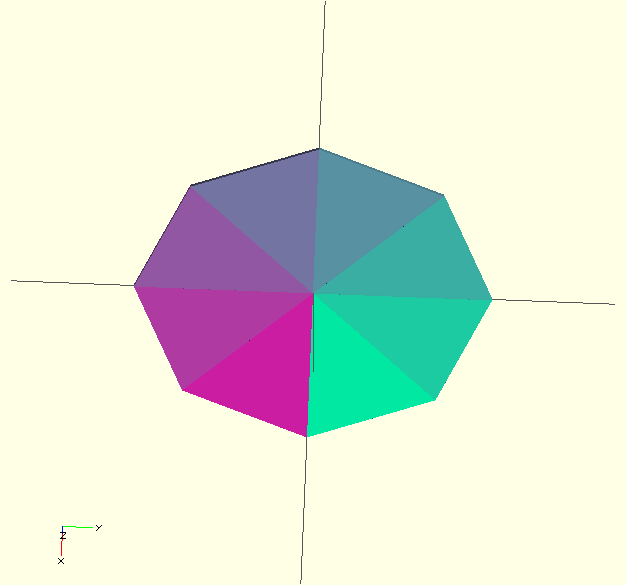
So for example we can generate the area inside a ellipse with :
module ellipse(R, e, n=10) {
function x(R,e,theta) = R * cos(theta);
function y(R,e,theta) = R *e * sin(theta) ;
assign(dth = 360/n)
for ( i = [0:n-1] ) {
assign (col = [i /n,1-i/n, 0.7]) {
echo(col);
color(col)
polygon(
[
[0,0],
[x(R,e,dth*i), y(R,e,dth*i)],
[x(R,e,dth*(i+1)), y(R,e,dth*(i+1))]
] );
}
}
}
ellipse(20,1.2,n=8);
Note that the functions x(0 and y() are local to the ellipse module. Modules can be declared within another module too, an undocumented feature which is very useful for modularisation.
Now we have the 2-D object, we can extrude it: linear_extrude to create a column, rotate_extrude to create a solid of revolution. Linear_extrude allows the shape to be rotated along the z axis using the 'twist parameter: eg:
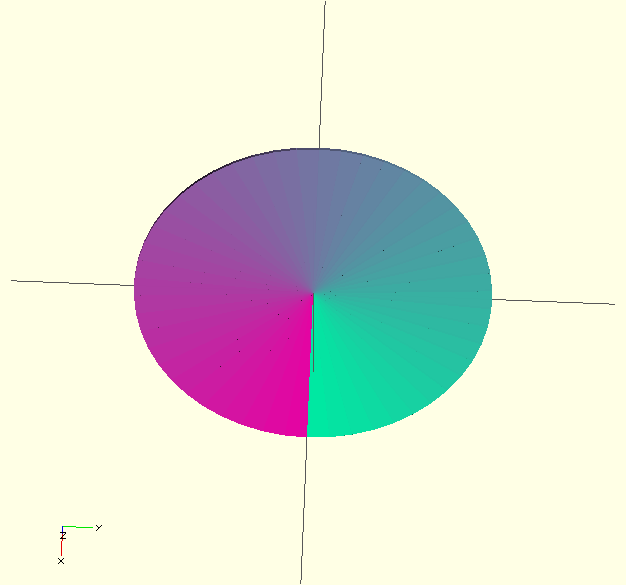
linear_extrude(height=30,twist=360) ellipse(20,1.5,n=50);
If we want an outline, we could place different polygons around the curve. Rather than the full segment, we could add a part of the segment nearest the curve:
module ellipse_rim(R, e, f,n=10) {
function x(R,e,theta) = R * cos(theta);
function y(R,e,theta) = R *e * sin(theta) ;
assign(dth = 360/n, Rf = R *(1- f))
for ( i = [0:n-1] ) {
assign (col = [i /n,1-i/n, 0.7]) {
echo(col);
color(col)
polygon(
[
[x(Rf,e,dth*i), y(Rf,e,dth*i)],
[x(R,e,dth*i), y(R,e,dth*i)],
[x(R,e,dth*(i+1)), y(R,e,dth*(i+1))],
[x(Rf,e,dth*(i+1)), y(Rf,e,dth*(i+1))]
] );
}
}
}
$fa=0.01; $fs=2.0;
ellipse_rim(20,1.5,0.2,n=20);
Here the width of the rim is a fixed proportion of the distance of the point from the origin, so the width varies. It would be better to have a fixed width rim but I haven't worked out the geometry yet.
Superellipse
We can use this technique to create superellipses:
module superellipse(R, p, e=1 , n=50) {
function x(R,p,e,a) = R * pow(abs(cos(a)),2/p) * sign(cos(a)) ;
function y(R,p,e,a) = R *e * pow(abs(sin(a)),2/p) * sign(sin(a)) ;
assign(dth = 360/n)
for ( i = [0:n-1] )
polygon(
[
[0,0],
[x(R,p,e,dth*i), y(R,p,e,dth*i)],
[x(R,p,e,dth*(i+1)), y(R,p,e,dth*(i+1))]
] );
}
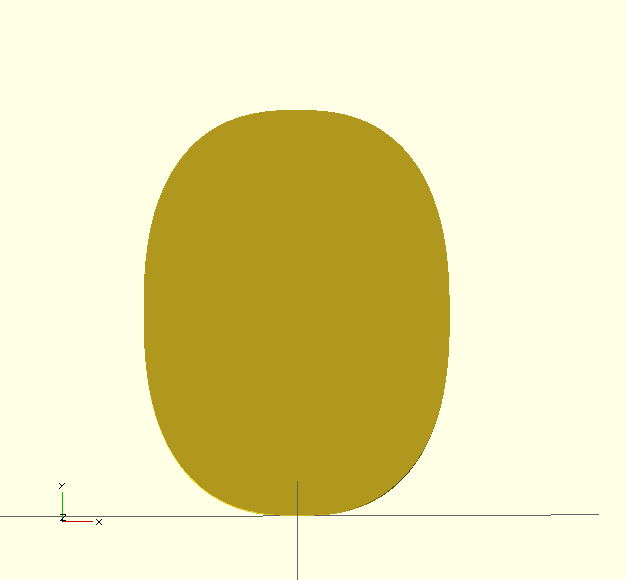
superellipse(20,2.5,0.75);
and we can use the animation feature to see how p affects the shape:
p = $t* 5; superellipse(20,p,0.75);
The super ellipse family includes some special case:
- p tends to 0, converges to cross-lines
- p = 2/3 is the astroid curve
- p = 1 is a square
- p = 2 is a circle
- p = 2.5 is Piet Hein's super circle
- p = 4 is a squircle
- p tends to infinity converges to a square