Neo-classical architecture and openscad
On Friday night we were lucky to get tickets to a concert by the Orchestra of the Age of Enlightenment at St George's in Bristol. The orchestra was lead by the violinist Kati Debratzeni in performances of Vivaldi's Four Seasons with additional works by Vivaldi and Teleman. The bass Matthew Rose sang exerpts from two of Vivaldi's operas and a tragic song about a pet canary eaten by a cat. A delightful and amusing evening.
Excellent though the music was, I couldn't help notice the fluted Doric columns which support the gallery and other architectural features of this neo-classical church. I confess that now I'm learning OpenSCAD, I see the world differently. Now every object becomes an exercise in solid constructive solid geometry.
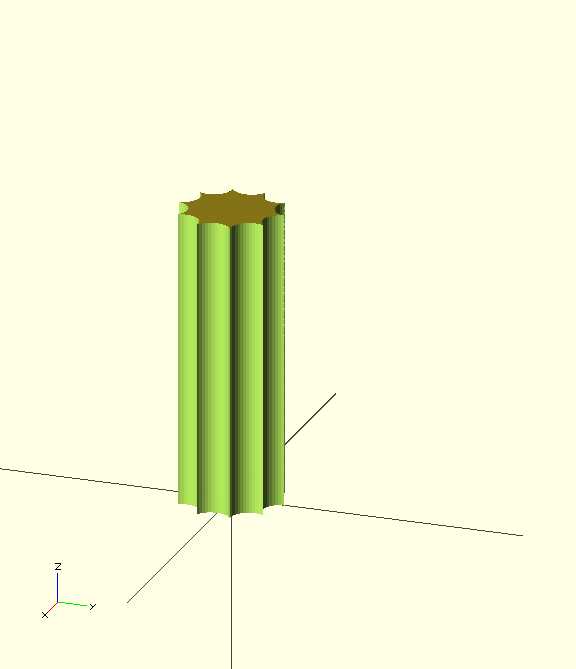
Fluted Columns
First a straight fluted column. This looks like a main column with a number of smaller columns removed around the circumference:
pi = 3.14159265359;
module column(radius,height) {
cylinder(r=radius,h=height,center=true);
}
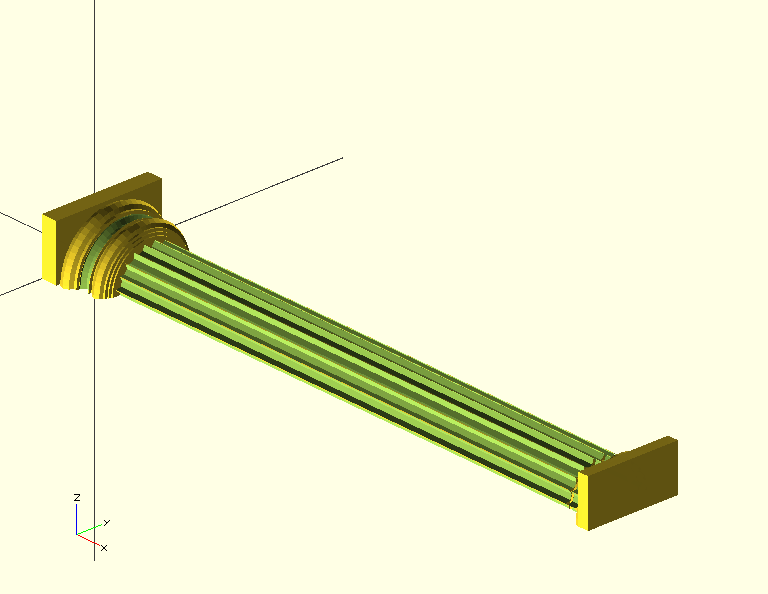
module fluted_column(radius,height,nflutes) {
assign( circumference = 2 * pi * radius)
assign (flute_radius = circumference /(2 *nflutes) )
{
echo("flute_radius",flute_radius);
translate([0,0,height/2])
difference () {
cylinder(r= radius, h =height, center=true);
for (i = [1:nflutes]) {
rotate( [0,0,i *360 /nflutes])
translate([radius,0,0])
column(radius=flute_radius,height=height+$delta);
}
}
}
}
fluted_column(radius=10,height=50,nflutes=10);
Variations of fluted columns include:
- the ends of the flutes may be 'stopped', i'e. terminating in a half round at one or both ends
- the ridge between the flutes ( the 'arris') may be flattened
- the column can be tapered and shaped
pi = 3.14159265359;
module capped_column (r1,r2,height,caps=0,delta=0) {
if (caps==0) { //none
cylinder(r1=r1,r2=r2,h=height+delta,center=true);
}
if (caps==1) // top
union() {
translate([0,0,-r2/2])
cylinder(r1=r1,r2=r2,h=height-r2,center=true);
translate([0,0,height/2-r2-delta]) sphere(r2);
}
if (caps==2) // bottom
union() {
translate([0,0,r1/2])
cylinder(r1=r1,r2=r2,h=height-r1,center=true);
translate([0,0,-(height/2 -r1-delta)]) sphere(r1);
}
if (caps==3) // both
union() {
cylinder(r1=r1,r2=r2,h=height-r1-r2,center=true);
translate([0,0,-(height/2 - r1-delta)]) sphere(r1);
translate([0,0,height/2 - r2-delta]) sphere(r2);
}
}
module tapered_fluted_column(r1,r2,height,nflutes=20,arris=0,caps=0,delta=0.2) {
assign(flute_r1 = (1 - arris) * pi * r1 / nflutes,
flute_r2 = (1 - arris) * pi * r2 / nflutes,
taper = atan((r1-r2)/height)
)
{
echo("flute_r1",flute_r1,"flute_r2",flute_r2);
translate([0,0,height/2])
difference () {
tapered_column(r1=r1,r2=r2, height =height);
for (i = [1:nflutes]) {
rotate( [0,0,i *360 /nflutes])
translate([(r1+r2)/2,0,0])
rotate([0,-taper,0]) // tilt the flute to align with the main column
capped_column(r1=flute_r1,r2=flute_r2, height=height, caps=caps,delta=delta);
}
}
}
}
tapered_fluted_column(r1=15,r2=13,height=150,nflutes=20,arris=0,caps=2);
A full Classical column
Typically, the main column stands on a base and is topped by an ornate capital. The designs of these parts of the column depend on the Order - Doric, Ionian, Coritinian - and whether Greek, Roman or Neo-classical. For Roman architecture, the rules for the profiles and proportions were set out by Vitruvius. in his classical work "De architectura" There is an online edition and translation of this text, for example this section on the construction of columns. I also found I had a reprint of James Newlands' The Carpenter's Assistant, published in 1860 which is a treasure-trove of constructions and terminology.
Here are just some of the decorations
- abacus - the square slab at the top beneath the lintel
- echinus - the decorated stone between the top of the column and the abacus - varies with order.
- hypotrachelion - the joint between the column and the capital
- attic base comprising various parts:
- torus - an rounded disk
- fillet - a straight-edged disk
- trocia - a concave profile
- slab
Each part can be modelled as a module. The base of each is on the x-y plane for ease of arrangement.
module slab(radius,height) {
translate([0,0,height/2])
cube([radius*2, radius*2,height],center=true);
}
module fillet(radius, height) {
translate([0,0,height/2]) cylinder(r=radius,h=height,center=true);
}
module trocia (radius, height,offset) {
assign(trocia_radius = height/2)
translate([0,0,trocia_radius])
difference() {
cylinder(r=radius,h=height,center=true);
rotate_extrude(convexity = 10)
translate([radius+offset, 0, trocia_radius])
circle(r = trocia_radius);
}
}
module torus(radius, height) {
assign(torus_radius =height/2)
assign(inner_radius = radius - torus_radius) {
echo("torus_radius",torus_radius);
translate([0,0,torus_radius]) {
rotate_extrude(convexity = 10)
translate([inner_radius, 0, 0])
circle(torus_radius);
cylinder(r=inner_radius,h=height,center=true);
}
}
}
Arranging the parts in order to build the column is tedious because each needs to be translated to its appropriate height up the column. To make this somewhat easier, this transformation uses a vector of separations (usually the heights of the parts) which are progressively summed with a recursive function to position each child object in turn.
function v_sum_r(v,n,k) =
k > n ? 0 : v[k] + v_sum_r(v,n,k+1);
function v_sum(v,n) = v_sum_r(v,n-1,0);
module stack (separations) {
union() {
for (i = [1:len(separations)]) {
assign(offset = v_sum(separations,i)) {
echo("i",i,"offset",offset);
translate ([0,0,offset]) child(i-1);
}
}
}
}
Transformations are a surprising and powerful feature of the language and turn out to be useful for many tasks. For example, if a part is a truncated torus we can write transformations like:
max=200;
module bottom(x) {
difference() {
child(0);
translate([0,0,max+x]) cube(2*max,center=true);
}
}
module top(x) {
difference() {
translate([0,0,-x]) child(0);
translate([0,0,-max]) cube(2*max,center=true);
}
}
and then compute a truncated torus with:
bottom(3) torus (17,6);
Now we can construct a complex column. The following is more ornate that those at St Georges. It has an attic base with an untapered fluted column, a hypertrachium and a simple Doric capital:
stack( [0,6,5,1,4,1,4,0.5,0.5,0.5,185,1,5,1,3]) {
// first an attic base
slab(20,6);
torus(20,5);
fillet(18,1);
trocia(17,4,0);
fillet(16,1);
torus(18,4);
fillet(16,0.5);
fillet(15,0.5);
fillet(14,0.5);
// then the fluted column
tapered_fluted_column( r1=13,r2=13,height=185,caps=0);
fillet(11,1); // hypertrachelium
tapered_fluted_column( r1=13,r2=13,height=5,,caps=1);
fillet(13,1);
// the echinus - bottom half of torus
bottom(3) torus (17,6);
// the abacus
slab(17,4);
}
Printing the column in this form may not be practical, so it may have to be printed in two halves., or a half used as a facade. The facade transformation rotates tthe child through 90 degrees and removes everything in the negative z region:
module facade () {
difference() {
rotate([0,90,0]) child(0);
translate([max-1,0,-max]) cube (2*max,center=true);
}
}
(I find the F5 rendering gets confused but the full render is OK. The full code is on GitHub and also in Thingiverse.
Reflection
I am amazed by the quality of the 3-d images of Greek architecture available on turbosquid eg. this Corinthian column and rather less so by the attempts to use Sketchup eg. this one. However these are complete models. With OpenSCAD, we can produce a fully parameterized kit for column construction. However, this code produces only a crude approximation: columns are not merely tapered but also bowed outwards slightly "entasis" , profiles are not simply circular curves, particularly in Greek architecture and capitals in the Ionic and Corinthian orders are very ornate. But if nothing else, the attempt to model classical columns has taught me much more about the structure and terminology of this architecture and I see now with a slightly more informed eye.
PS
I've since found some prior work on columns on Thingiverse: This for creating a Doric temple
http://www.thingiverse.com/thing:21868
and this on making a column with a varying profile
http://www.thingiverse.com/thing:23971
which might make it possible to include entasis although I dont yet see how to make the column evenly fluted as well - perhaps by fluting each cone /blog