OpenSCAD, the Minkowski sum and a heart-shaped box
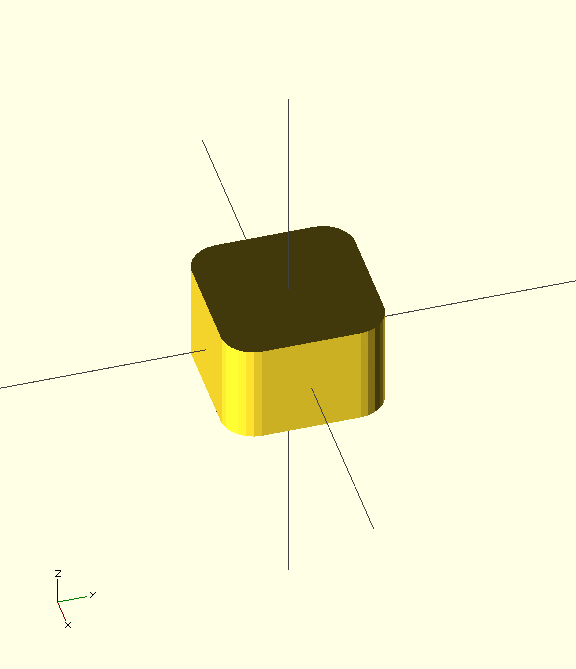
In my exploration of openSCAD, the Minkowski sum looks interesting. The example given in the Wikibook is of rolling the z-axis edges of a cube:
minkowski() {
cube(12,center=true);
cylinder(r=4, h=1);
}
although for this task, it's faster to do the minkowski operation in 2-D and then extrude:
linear_extrude(height=20)
minkowski() {
square(12,center=true);
circle(r=4);
}
In both cases, the result is a cube of size 20 - the inner cube of size 12 + 2 * 4, the radius of the circle or cylinder
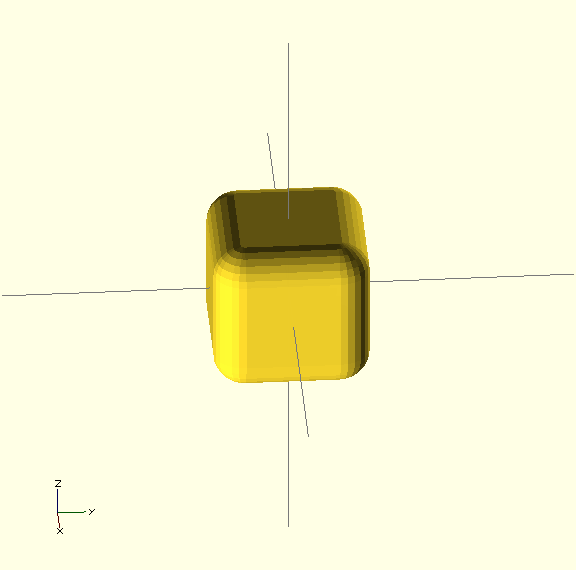
If we want to roll all edges:
minkowski() {
cube(12,center=true);
cylinder(r=4, h=1);
rotate([90,0,0]) cylinder(r=2, h=1);
rotate([0,90,0]) cylinder(r=2, h=1);
}
but this takes a minute on my basic laptop to run.
More simply, we can roll all edges by summing with a sphere instead of a cylinder although this takes longer to run:
minkowski() {
cube(12,center=true);
sphere(r=4);
}
$fn=6;
minkowski() {
cube(12,center=true);
sphere(r=4);
}
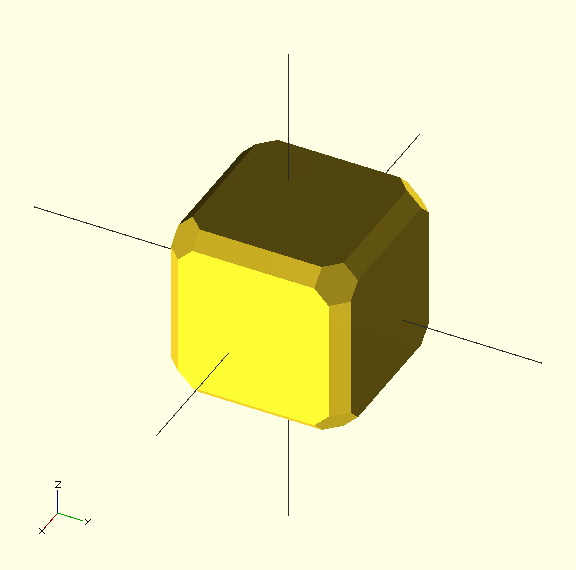
but this is not accurate. A precise approach uses a rotated cube. Here I've defined a module to parameterize the dimensions:
module chamfered_cube(s,c) {
minkowski() {
cube(s,center=true);
rotate([45,0,0]) cube(c);
rotate([0,45,0]) cube(c);
rotate([0,0,45]) cube(c);
}
}
chamfered_cube(20,4);
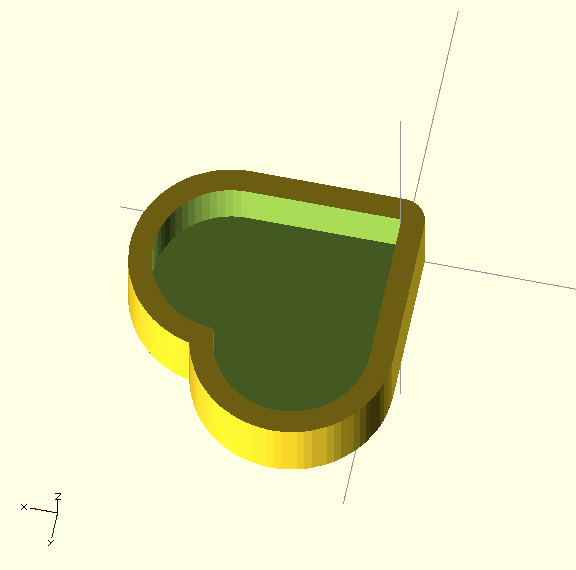
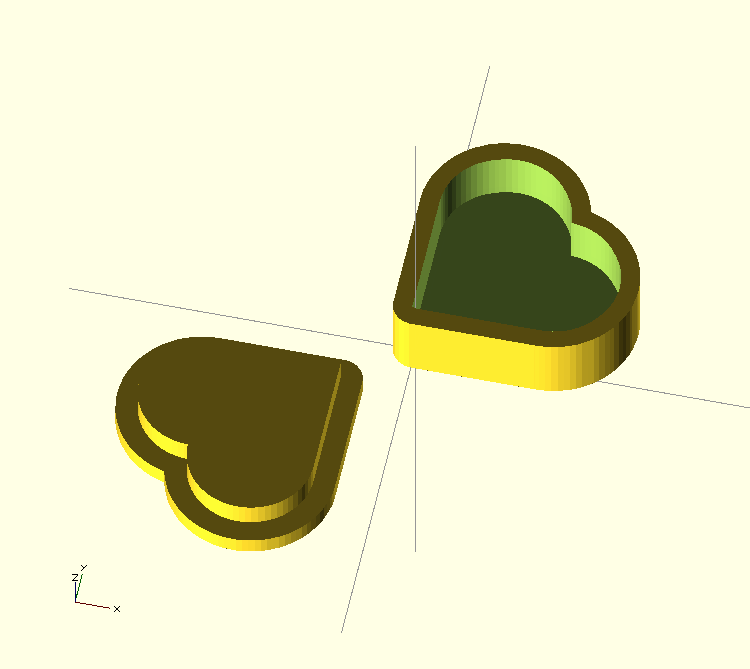
The main use I've seen so far for minkoski operator is to create a cookie cutter. Here the operator is used to add a constant width boundary around an arbitrary curve. One of my projects was to make a heart-shaped box, but my first attempts to remove the box inside with a scaled version of the outside yielded odd wall thicknesses. Minkowski is the way to go for irregular shapes.
module heart_shape(size) {
union() {
square(size,size);
translate([size/2,size,0]) circle(size/2);
translate([size,size/2,0]) circle(size/2);
}
}
module heart(size,thickness,height) {
linear_extrude(height=height)
minkowski() {
heart_shape(size);
circle(thickness+0.1); //because 0 would produce an empty object
}
}
module heart_box(size,height,thickness) {
difference() {
heart(size,thickness,height);
translate([0,0,thickness]) heart(size,0,height);
}
}
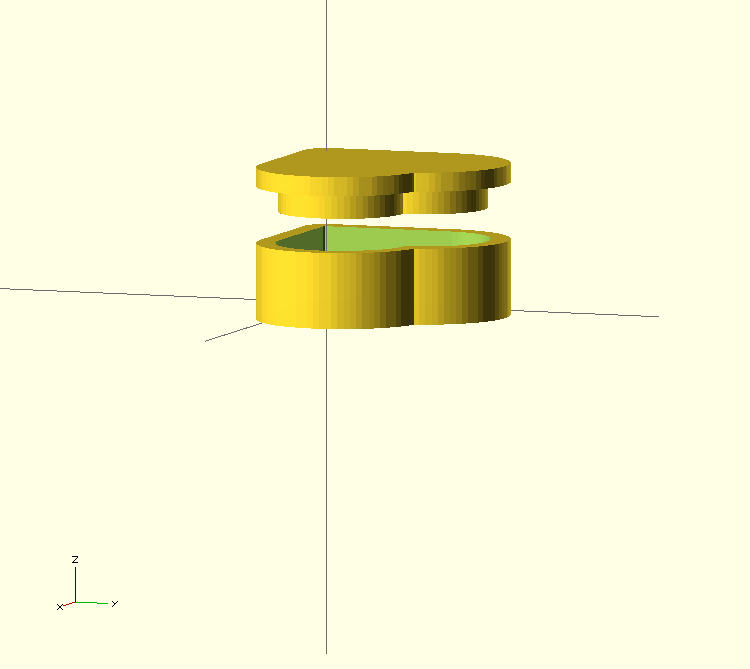
heart_box(20,10,3);
The Minkowski sum is used to add a thickness of 3 mm either side of the heart-shaped boundary, giving a wall thickness of 2 * 3. The heart-shape is offset by the thickness for the outside and by zero for the inside of the box, leaving a constant wall thickness of 3.
Making a box and lid, with clearance between box and lid proved a bit trickier. I found the most accurate approach was to start with a heart shape sized to the inside of the lid, requiring 4 shapes with different boundary thicknesses:
- inside lid : 0
- outside lid : thickness + clearance
- inside box : clearance
- outside box : thickness + clearance
I had this printed on a Makerbot and it looks rather good. The lid is a little sloppy and the depth of the inset is too shallow, so some adjustment is needed.