Gothic architecture and OpenSCAD
I've often thought about the geometry of Gothic architecture and how one might describe a particular window or doorway, like the Royal Portal at Chatres mathematically.
With OpenSCAD, I have a language both to descibe the geometry and print a model. A full Gothic cathedral kitset might be some way off but I will make a start on a simple arched doorway.The essence of Gothic architecture as a development from Norman architecture is the use of pointed arches in place of rounded arches. The arcs of the arch have centres offset from the centre-line. If the offset is 0 you have a Norman arch, the greater the offset the more pointed:
module arch(x,y,r,d) {
linear_extrude(height=d)
union() {
intersection () {
translate([x,y,0]) circle(r);
translate([-x,y,0]) circle(r);
}
translate([0,y/2,0]) square(size=[2 *(r-x), y],center=true);
}
};
where x is the offset, y the height to the start of the arch (the 'springing point') , r the radius of the arc and d the depth of the arc in the z dimension.
With this object, we can make an archway by removing a smaller inner arch from a larger outer arch:
module archway(x,y,r,d,t) {
difference () {
arch(x,y,r,d);
translate([0,0,-1]) arch(x,y,r-t,d+ 2);
}
}
and with that object, a nest of archways:
module nested_archway (x,y,r,d,t,n) {
union() {
for (i=[0:n-1]) {
archway(x,y,r+i*t,d+i*t,t);
}
}
}
Here the achways have the same thickness and constantly increasing depth. However, real nested arches have different thicknesses and depths which we could descibe as vectors. Whilst the depth values can be absolute, we need to be able to accumulate the thicknesses so that the arc radius can be increased by the cumulative thickness. Since OpenSCAD is a functional language, we cant accumulate the thickness by assignment so we need to compute this sum with a recursive function:
function v_sum_r(v,n,k) =
k > n ? 0 : v[k] + v_sum_r(v,n,k+1);
function v_sum(v,n) = v_sum_r(v,n-1,0);
so v_sum([1,2,3,4],3) sums the first 3 terms of the vector and returns 6.
Now we can express a nested arch with differing depths using two vectors, one of successive thuicknesses, the other of absolute depths:
module variable_nested_archway (x,y,r,d,t,n) {
union() {
for (i=[0:n-1]) {
assign(dt = v_sum(t,i+1) ) {
echo(dt);
archway(x,y,r+dt,d[i], t[i]);
}
}
}
}
so now
variable_nested_archway(2,10,6,[1,3,4],[1,3,1],3);
creates a three-arch doorway with the second arch much thicker and deeper than those on either side.
These objects are actually a bit messy in the negative y area. OpenSCAD supports generic transformations so we can make a transform to remove everything in that area:
module remove_ground() {
difference() {
child(0);
translate([0,-50,0]) cube([100,100,100],center=true);
}
}
so now
remove_ground()
variable_nested_archway(2,10,6,[1,3,4],[1,3,1],3);
cleans up the base of the arch.
Here the parameters for an arch are expressed in coordinates rather than in architectural terms. A pointed arch is designed to fill a rectangle so the parameters should be the height and width of this space, and the sharpness of the point, from which the height to the springing point, the offset and the radius can be computed.
The pointed arch is based on a tangent ogive in which the arc is tangent to the vertical where it meets the vertical. Given a length and base of the arc, the radius is given by length^2 + base^2 / 2 * base. The sharpness of the curve is the ratio of the length to the overall width i.e 2 * base, so a sharpness of 0.5 would be a circular arc. The classic arch is called a quinto acuto and has a sharpness of 4/5 whilst the recto arch or equilateral arch has a sharpness of 1.
module ogive_arch(width,height,sharpness,depth) {
assign(base=width/2, length = width * sharpness)
assign(radius = (base * base + length * length) / (2 * base))
assign(x= radius - base,y = height-length)
arch(x,y,radius,depth);
}
Now as we change the sharpness, the space filled by the arch remains the same. Note that multiple assign statements are needed because within an assignment, the set of expressions is not ordered, so all variable used must be already assigned values.
The code is in GitHub
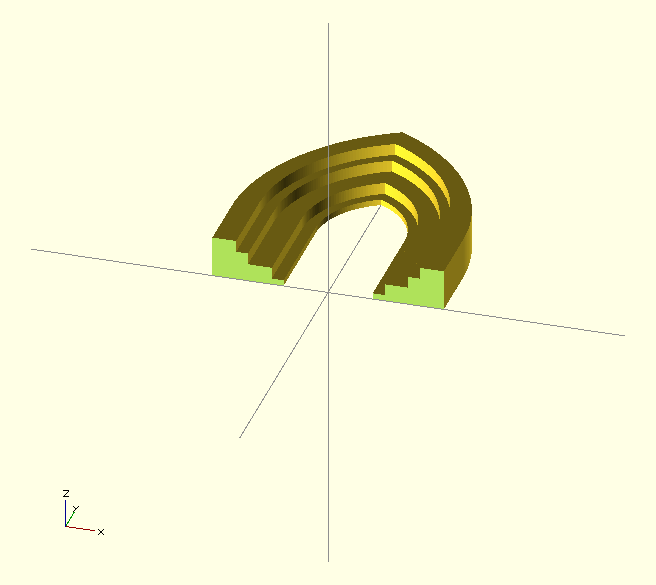
This piece was created by that code:
A problem I often encounter is when to move from 2D to 3D by extrusion. Here I extruded when making the arch shape but should I delay extrusion untill I need to use a 3D operation? It seems better and faster to stay within 2D as long as possible, so the code in GitHub delays extrusion until a solid is needed.
Next step will be to design a Gothic window, with multiple lancets, trefoils and quadrafoils. For my first attempt, I had to visually place and size the infills so more geometry needed now. There is some useful material around. The paper "Generative Parametric Design of Gothic Window Tracery" looks very relevant as does this ebook Tips and Tricks to Gothic Geometry. I think I've just discovered a great way of avoiding work.
Postscript.
Looking again at this nested arch, I realized that it was quite wrong: each arch has the same sharpness but as a consequence the thickness varies and this looks very wrong. I reworked the script so that either the outer or inner dimensions can be specified as width, height and sharpness but each arch is generated with the x,y,radius coordinates by varying the radius. Now the sharpness changes as the arches get wider as you would expect. The revised code is in GitHub and the picture shows the revised arch. Writing a function to calculate the x,y,radius parameters is hampered by the limited function syntax, in particular that only a single expression is allowed and assign() is not allowed.