3D printing, OpenSCAD, intersections and animation
A friend's Christmas present to himself (and indirectly his family and friends) was a MakerBot Replicator 3-D printer. Down at Bristol Hackspace we have several repraps in various stages of completion, but none yet ready for novice use. Marc's printer seems to have worked out of the box, so I was able to get my first test piece send via Dropbox to London, printed appropriately enough, since it involved hearts, in a pretty pink plastic and posted to Bristol in a couple of days.
The key to my personal progress was the discovery of OpenSCAD. I've looked at using GUI-based 3-D tools like Blender but OpenSCAD is a programming environment, just my kind of 3-D tool. I soon found a weath of freely avaliable tutorials, reference material and scripts:
- RepRap Introduction - good starting point
- Wikibook Useful reference but needs work to update resources
- Thingiverse a wealth of libraries and designs
- GitHub where many libraries are maintained
OpenSCAD uses two modes of construction: Constructive Solid Geometry (CSG) using the Computational Geometry Algorithms Library (CGAL); and extrusion(two modes) of a 2-D shape.
Some lessons learnt:
- this is a functional langugae, so a variable cannot be udated, although it can be rebound with the assign() statement
- semicolons are statement terminators, not separtators
- vectors are immutable, so you can't dynamically construct a vector; This is a nuisance because you can't dynamically construct a polygon or polyhedron so scad files have to be generated by a more expressive language like Python.
- variable, module, and function names can't contain "-"
- CSG operators are union(), difference() and intersection() and special operators minkowski() and hull()
- 3-D transformations are transform(), scale(), rotate(), mirror() and the general multmatrix()
- 2-D objects are constructed from the 2-D primitives square, circle and polygon and imported DXF files
- 3-D objects are constructed from the 3-D primitives cube, cylinder, sphere and polyhedra and by extrusion of 2-D objects
- complex objects are defined using parameterised modules
- modules may invoke other modules, but there must be no cycles so recursion is not permitted
- a module may be defined as a generic transform by acting on "child" nodes. This allows the module to be used in a chain of transformations rather than as an atomic object.
- scalar functions are supported but the body is a simple expression
The challenge for the budding designer is to learn how to compose a desired shape by the application of the operators to the primitives. In the physical world, we typically construct objects in a 'carpentry' mode, glueing non-intersectiing objects (union) and removing waste (difference). Also our range of primitives is vast and I generally have no idea how, say, a nut is formed. CSG allows us to union() overlapping objects, get the intersection of objects and use the less-known operators minkowski sum and hull. To see what experienced openSCAD programmers use, I analysed the collection of 22 library files for basic shapes, gears and threads etc. There were a total of 10000 lines including comments. I used grep to do the counting of patterns such as 'rotate\s*(' to get counts of each construct in the language.
- Transformations
translate 1088 rotate 625 scale 576 mirror 3 multmatrix 0 - CSG operators
union 576 Severe underestimate since union() is the default for a sequence of objects difference 36 linear_extrude 18 intersection 9 intersection_for 2 replacement for loop within intersection which doesnt work
rotate_extrude 2 projection 1 minkowski 0 hull 0 - 2-D primitives
polygon 19 circle 10 square 5 - 3-D primitives
cylinder 1029 cube 52 polyhedra 45 sphere 15 surface 0 - language elements
function 144 module 111 assign 43 if 41 for 38 echo 20 include 4 use 2 search 0 str 0 concatenate
Exploring Intersection
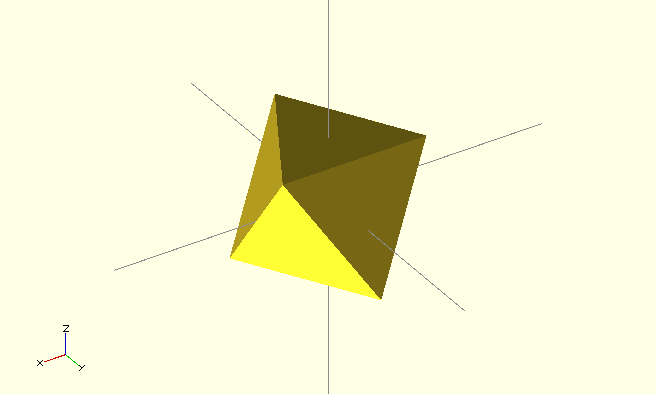
This data seems to indicate that designers are mainly using operators which correspond to the physical operations (carpentry mode) and are generally not using the advanced operators. This is not surprising because even intersection can yield surprising results. An example in the wikibook shows the construction of a dodecahedron from the intersection of 6 boxes:
but I havent been able to trace the source of this construction. It's tempting to look for ways of constructing the other regular solids using intersection and indeed playing with this code, I found I could make an octahedron:
Animation
What other solids could I make this way? One feature of OpenSCAD is very useful here - the ability to display a parameterized sequence of objects as an animation. The system variable $t changes from 0 to 1 in increments determined by the total number frames entered in the animation panel, so to see what solids are generated as the dihedral angle is changed :
and its fun to watch the shapes morph, becoming dodecahedrons at several angles and curious asymmetric faceted shapes in between. Moreover you can edit the script as it runs to change other parameters such as the number of intersecting boxes. You can also create a video. Each frame is saved as a .png file. I used ffmpeg installed on Ubuntu:
> ffmpeg -f image2 -i frame%05d.png -r 12 dodec.avi
to create this little video